raton

CALCULAR AREAS Y VOLUMENES Y CONSTRUIR DESARROLLOS DE PLANOS DE     CUBOS ,PRISMAS Y PIRAMIDES RECTOS

Introducción

Este documento está dirigido a los estudiantes quienes an sido piesa importante para realisar este trabajo, el cual ba encaminadado para que los jovenes de secundaria puedan  tenr una amyo  realicen Proporciona a los alumnos la información básica sobre la actividad, les orienta sobre lo que les espera y suscita y mantiene su interés mediante una formulación atractiva. Los proyectos deben presentarse haciendo que los temas sean atractivos, visualmente interesantes, relevantes para los alumnos en función de sus experiencias pasadas o de sus metas futuras, importantes por sus implicaciones globales, urgentes porque necesitan una pronta solución, o divertidos ya que ellos pueden realizar algo o desempeñar un papel. El propósito de esta sección es preparar a los lectores y despertar su interés por la tarea, no contar todo lo que hay que hacer.

Tarea

Como resultado final se espera que los alumnos:

• Anticipen diferentes vistas de un cuerpo geométrico.

• Resuelvan problemas en los que sea necesario calcular cualquiera de los términos de las fórmulas para obtener el volumen de prismas y pirámides rectos. Establezcan relaciones de variación entre dichos términos.

 

Curso: Matemáticas 2        Apartado: 2.3                      Eje temático: FEyM

Conocimientos y habilidades: Describir las características de cubos, prismas y pirámides. Construir desarrollos planos de cubos, prismas y pirámides rectos. Anticipar diferentes vistas de un cuerpo geométrico.

Intenciones Didácticas:

Que los alumnos dibujen cuerpos geométricos como cubos, prismas y pirámides, con base en las características dadas por escrito.

Curso: Matemáticas 2                   Bloque: 2                 Eje temático:    FEyM       

Conocimientos y habilidades: Justificar las fórmulas para calcular el volumen de cubos, prismas y pirámides rectos.

Intenciones didácticas: Que los alumnos relacionen el volumen del cubo y algunos otros prismas con sus respectivas dimensiones, para justificar sus fórmulas mediante procedimientos personales.

Proceso

Sugerencia de como contestar los ejercisios anteriores

•   Organizados en parejas,encuentren  el volumen de los ejecicios anteriores
• formados en equipos de 4 personas armar las figuras  anteriores 

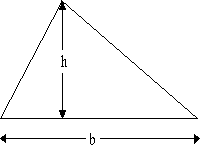El triángulo es un polígono formado por tres lados y tres ángulos.
La suma de todos sus ángulos siempre es 180 grados.
Para calcular el área se emplea la siguiente fórmula:
 

Área del triángulo = (base * altura) /

Evaluación

1Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho y 2500 mm de alto.
2Una piscina tiene 8 m de largo, 6 m de ancho y 1.5 m de profundidad. Se pinta la piscina a razón de 6 € el metro cuadrado.

1Cuánto costará pintarla.

2Cuántos litros de agua serán necesarios para llenarla.

3En un almacén de dimensiones 5 m de largo, 3 m de ancho y 2 m de alto queremos almacenar cajas de dimensiones 10 dm de largo, 6 dm de ancho y 4 dm de alto. ¿Cuantas cajas podremos almacenar?
4Determina el área total de un tetraedro, un octaedro y un icosaedro de 5 cm de arista.
5 Calcula la altura de un prisma que tiene como área de la base 12 dm² y 48 l de capacidad.
6 Calcula la cantidad de hojalata que se necesitará para hacer 10 botes de forma cilíndrica de 10 cm de diámetro y 20 cm de altura.
7Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Y la altura mide 125.66 cm. Calcular:

1 El área total.

2 El volumen

8En una probeta de 6 cm de radio se echan cuatro cubitos de hielo de 4 cm de arista. ¿A qué altura llegará el agua cuando se derritan?
9 La cúpula de una catedral tiene forma semiesférica, de radio 50 m. Si restaurarla tiene un coste de 300 € el m², ¿A cuánto ascenderá el presupuesto de la restauración?
10¿Cuántas losetas cuadradas de 20 cm de lado se necesitan para recubrir las caras de una piscina de 10 m de largo por 6 m de ancho y de 3 m de profundidad?
11Un recipiente cilíndrico de 5 cm de radio y y 10 cm de altura se llena de agua. Si la masa del recipiente lleno es de 2 kg, ¿cuál es la masa del recipiente vacío?
12Para una fiesta, Luís ha hecho 10 gorros de forma cónica con cartón. ¿Cuánto cartón habrá utilizado si las dimensiones del gorro son 15 cm de radio y 25 cm de generatriz?
13Un cubo de 20 cm de arista está lleno de agua. ¿Cabría esta agua en una esfera de 20 cm de radio?

 14 Hacer un cubo de 10cm*10cm*10cm

 15 Hacer un triangulo que mida 100cm de base y 10 de altura

Conclusión

 Al terminar de resolver estos ejercicios el alumno podra encontrar areas y volumenes de cualquier figura geometrica y al mismo tiempo desarrollara su capacidad espacial y su abilidad  para representar cuerpos geometricos

cuerpos geometricos.
 prisma
 area de un triangulo

Créditos y Referencias

http://www.reformasecundaria.sep.gob.mx/matematicas/index.htm
http://www.vitutor.net/2/2/6.html
http://aulavirtual.inaeba.edu.mx/ejercicios_practicos/paginas/ejercicios_sec_mate.html